asignacion # 2 Mediciones Industriales

MEDICIONES INDUSTRIALES

TEMA II: SENSORES MODULADORES
Sumario:
1. Sensores resistivos.
1.1. Potenciómetros (Variables mecánicas)
1.2. Galgas extensométricas (Variables mecánicas)
1.3. Termorresistencias (Variable térmicas)
1.4. Termistores (Variables térmicas)
1.5. Magnetorresistencias (Variable magnéticas)
1.6. Fotorresistencias (Variables ópticas)
1.7. Higrómetros resistivos (Variables químicas)
1.8. Acondicionamiento: Puente de Wheatstone, Amplificador de Instrumentación.
2. Sensores de reactancia variable
2.1. Sensores Capacitivos
2.1.1. Condensador variable
2.1.2. Condensador diferencial
2.1.3. Acondicionamiento: divisor de tensión, amplificador de carga, amplificador de transconductancia
2.2. Sensores inductivos
2.2.1. Reluctancia variable
2.2.2. Inductancia mutua (LVDT)
2.2.3. Acondicionamiento
3. Sensores electromagnéticos
3.1. Basados en la ley de Faraday
3.2. Basados en el efecto Hall


Sensores Moduladores

Los sensores moduladores son aquellos que varían un parámetro eléctrico en función de la variable a medir. La variable puede ser presión, temperatura, caudal, etc., y el parámetro eléctrico
puede ser resistencia, inductancia, capacitancia o campo magnético o eléctrico. La clasificación general de esto sensores se hace en Sensores resistivos y sensores de reactancia variable.
1. Sensores resistivos.
Los sensores moduladores del tipo resistivos, son aquellos que varían una resistencia en función de la variable a medir. Se ha realizado una clasificación de estos sensores en función de la variable a medir, tal como refleja la tabla siguiente:

1.1. Potenciómetros (Variables mecánicas)
El potenciómetro es un sensor utilizado para medir la variable mecánica desplazamiento, y consiste de un dispositivo con dos partes y tres terminales.
Una de las partes es una resistencia fija descubierta la cual puede ser de carbón o de hilo arrollado.
La otra parte es un contacto móvil que se desplaza por la resistencia fija.
En Teoría, para un conductor cualquiera, su resistencia viene dada por:

Donde:
ρ = Resistividad del material (Ωm)
A = Sección transversal
l = Longitud del conductor.
En la figura siguiente se muestra el modelo de un potenciómetro. Si se denomina x a la distancia recorrida por el curso, la resistencia obtenida será:
El problema de este tipo de sensor es:
a. Varía con la temperatura.
b. Varía con la deformación de la sección transversal, causada por la presión o fuerzas ejercidas sobre el.
c. El contacto del cursor origina desgaste, modificando la sección transversal.
Pueden ser lineales, como la figura mostrada anteriormente, o no lineales como el siguiente:
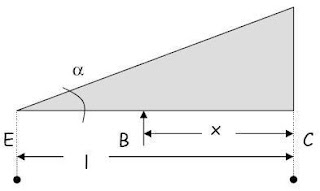En este último caso, la resistencia fija entre E y C está formada por una sección triangular variable de hilo arrollado. Este hilo tiene una sección A y diámetro D.
La ecuación de su resistencia es ahora:
Los potenciómetros pueden dar una salida analógica, si la resistencia fija es de carbón, o digital, si la resistencia fija está formada por hilo arrollado.
El potenciómetro se utiliza para medir preferiblemente desplazamientos, conectando el objeto de medición a su cursor. Sin embargo, puede ser utilizado para medir otras variables de forma indirecta, cuando estas generen desplazamientos en otros dispositivos.
Por ejemplo:
a. Se puede utilizar para medir presión, si se conecta el cursor al extremo de un tubo Bourdon.
b. Para medir nivel en líquidos conductores o no conductores.
c. Para medir temperatura si se conecta al extremo de un medidor de bulbo y capilar.
En los casos a y c se utiliza para generar una señal eléctrica. Mientras que en el caso b es el elemento primario.

1.2. Galgas extenso métricas (Variables mecánicas)
Se basan en el efecto piezorresistivo ya descrito para el potenciómetro. LA diferencia es que ahora se busca modificar la resistencia variando algunos de los parámetro de la resistencia, por ejemplo, su longitud l o su sección transversal A.
Si a una pieza de material resistivo se le aplica un esfuerzo, esta se deformará, y cambiará su resistencia. Por tanto, este tipo de sensores se utiliza para medir fuerza o presión, aunque también puede aplicarse a la medida de desplazamientos pequeños.
Todo material al que se le aplica un esfuerzo se deformará en mayor o menor grado, y llegará a un punto en que se romperá. Esta relación esfuerzo vs deformación se muestra en la siguiente gráfica.
Si se tiene un conductor cilíndrico de longitud l y sección transversal A, y se le aplica un esfuerzo perpendicular a la sección transversal, de tal forma de comprimirlo o estirarlo, es decir,
Donde:
E = Constante del material o módulo de Young en Pa
σ = Tensión mecánica o esfuerzo en Pa o Kg/cm2
ε = Deformación unitaria adimensional, normalmente dada en μdeformaciones (10-6 m/m)
Este análisis tan simple no es aplicable para piezas tridimensionales, ya que al aplicar el esfuerzo en la dirección indicada es de esperar que también se altere la sección transversal A. Si denominamos D al diámetro involucrado, se debe definir un nuevo coeficiente: el coeficiente de Poisson, el cual viene definido como:
Se procederá a realizar un análisis de la relación de estas deformaciones con la resistividad del material.
Para los metales se cumple:
Donde C es la constante de Bridgman (1,13 a 1,15 para galgas)
El volumen del resistor cilíndrico indicado al principio es:
Sustituyendo (8) en (7)
Sustituyendo (9) en (6)
De (1)

Sustituyendo (11) en (10)
Como es un cilindro:
Sustituyendo (14) en (12)
K se denomina factor de sensibilidad de la galga.
Si los cambios en un sensor resistivo puede ser expresados como



Finalmente como de (4)
Los principales problemas de las galgas son:
a. Cuidar el margen elástico.
b. El esfuerzo debe ser totalmente transversal a la galga.
c. La temperatura altera su valor.
Ejemplos de galgas:
Las galgas se pueden aplicar a:
a. Medida de fuerza.
b. Medida de presión.
c. Medida de desplazamientos pequeños.
d. Medida de vibración.
1.3. Termorresistencias (Variable térmicas)

Una termorresistencia es un dispositivo que varía su resistencia con la temperatura. Suele denominarse RTD (Resistive temperature detector) por sus siglas en ingles.
El símbolo que la caracteriza es:
El símbolo sin flecha indica que la variación es intrínseca por la característica resistiva, no por manipulación manual.






La ecuación característica de las termorresistencia es la siguiente:
Este dispositivo tiene como limitaciones.
* No puede medir temperaturas próximas a la de la fusión del conductor con que se fabrica.
* El autocalentamiento ocasionará derivas en la medición.
* S se deforma, puede cambiar su patrón de medición.
Tiene como ventaja el ser diez veces más sensible que los termopares, tal como se verá más adelante.
Normalmente no es necesario considerar todos los coeficientes de la ecuación (19), sino que considerando solo el primer término se tiene una excelente aproximación, es decir,
Donde α es la sensibilidad del material, y R0 es la resistencia a la temperatura de referencia (normalmente 0 grados).
En la tabla siguiente se muestran las Termorresistencias típicas:
La termorresistencia mas común por su linealidad es la de platino, que se suele denominar.
Pt100 (termorresistencia de platino con R0 =100 Ω a 0° C)
Pt1000 (termorresistencia de platino con R0 =1000 Ω a 0° C)
1.4. Termistores (Variables térmicas)
Los termistores también son resistencias que varían su magnitud con la temperatura. Se diferencian de las termorresistencia por que están basadas en semiconductores. Por tanto su característica no es lineal, aunque dentro de un margen adecuado pueda ser considerada de es amanera.
Su símbolo será:
La raya quebrada indica que no es lineal. El elemento positivo o negativo indica que tiene una característica positiva o negativa respectivamente. Es decir, si es de coeficiente positivo, PTC, la resistencia se incrementa con la temperatura. Si es de coeficiente negativo, NTC, disminuye con la temperatura.
En el caso de una NTC la ecuación característica será
Donde:
B = temperatura característica del material (2000 K a 5000 K)
R0 = Resistencia a la temperatura de referencia T0, normalmente la temperatura ambiente
(25 °C o 298 K)
Tiene como ventajas el ser más sensible que las Termorresistencias, más rápidas y permite hilos de conexión mayores.
Tiene como desventaja el ser no lineal, y al variar su temperatura por el autocalentamiento del material.
Los termistores tienen muchas aplicaciones algunos de los cuales son.
a. Medida directa de temperatura por variación de corriente:









b. Medida de caudal en circuito puente.
c. Protección por autocalentamiento.
1.5. Magnetorresistencias (Variable magnéticas)
Las magnetorresistencias se basan en la variación de resistencia en un conductor por variaciones en el campo magnético. Este efecto se denomina efecto magnetorresistivo y fue descubierto por Lord Kelvin en 1856
Este tipo de sensores tiene la ventaja con respecto a los sensores inductivos, por ser de orden cero, y con respecto a los sensores de efecto Hall por ser más sensible y proveer un mayor margen de medición de medición.
Está formada por una aleación de Hierro y Níquel (permalloy)
Tiene las siguientes aplicaciones:
* Medición de campos magnéticos en las lectoras de tarjetas.
* Otras magnitudes que provean un cambio en el campo magnético, como el desplazamiento de una pieza, detectores de proximidad, nivel de flotador, etc. En estos casos se utiliza un imán que cambia su posición con el proceso. El campo generado por el imán es medido por la magnetorresistencia.
1.6. Fotorresistencias (Variables ópticas)
Las fotorresistencias o LDR, es un dispositivo que cambia su resistencia por el nivel de incidencia de luz. Esta formada por materiales semiconductores.
Su símbolo:
1.7. Higrómetros resistivos (Variables químicas)
El higrómetro se utiliza para medir humedad. Se basan en la variación de resistencia que experimentan los materiales por la humedad, como el vapor de agua en un gas o el agua absorbida en un líquido o sólido.
Un material típico es el aislante eléctrico, el cual disminuye su resistencia al aumentar su contenido de humedad.

1.8. Acondicionamiento de sensores resistivos
Los sensores resistivos deben ser conectados a circuitos de interfaz adecuado para poder aprovechar o medir el parámetro variado.
Tradicionalmente no se suele medir la resistencia que varía, sino la variación de otro parámetro que depende de esta, como la tensión, la corriente o la frecuencia.
En este capítulo nos centraremos en los circuitos de interfaz tradicionales, dejando la salida casi-digital o digital a capítulos posteriores.
Los métodos de acondicionamiento se clasificarán en tres grupos:
a. Divisor de tensión.
b. Puente de Weatstone
c. Amplificadores para puente de sensores.
Si en forma general se representa la variación de resistencia en un sensor resistivo como;
El margen de variación de estos medidores puede representar se como:
Todos estos sensores necesitan una alimentación eléctrica y presentan el problema que el autocalentamiento influye en la medida.
1.8.1 Divisor de Tensión:
Un divisor de tensión es una interfaz formada por una combinación serie de un resistor y un sensor, alimentados por una fuente de fija de tensión o corriente. Puede darse el caso que el sensor forme conforme la asociación serie de estos dos dispositivos.
En la siguiente figura se puede observar la aplicación de esta interfaz al caso de potenciómetros.
La ecuación del circuito será:


Si K = Rm/Rn y α = 1-x, entonces
Esta ecuación demuestra que el sistema será lineal solo si K tiende a ∞, lo cual ocurrirá si Rm >> Rn
Antes de continuar se debe destacar que la no linealidad en si debe representar un error.
Por ejemplo, un sensor no lineal dará una respuesta no lineal que no debe ser interpretada como un error de medida. En cambio, si un sensor lineal modifica su característica de salida por culpa de la interfaz, entonces si se puede hablar de error. El caso actual es un ejemplo de este tipo de errores.
Para calcular este error, tomemos en cuenta que:
Valor ideal = Rm tiende a ∞, por tanto, K tiende a ∞, por lo que Vi = V(1-x)
Valor real o medido = Vm de la ecuación (24),

El error será:
El error será máximo cuando
El error absoluto a fondo escala será:
Puede observarse que el problema de esta interfaz se centra en el efecto de carga que introduce el medidor (Rm). Una forma de corregirlo es usando medidores con Rm muy grande.
Otra forma es usando una Rm adicional tal y como muestra la siguiente figura
¿Cuanto vale Vm, y el error de media?
Revisar según el libro
En el caso de que se quiera aplicar esta interfaz a termistores, será necesario utilizar un resistor en serie con el termistor, y medir la caída de tensión en este resistor, a fin de compensar en parte la no linealidad del sensor.
1.8.2. Puente de Wheatstone:
El puente de Wheatstone es un dispositivo orientado a corregir parte del problema que presenta la configuración anterior: Linealidad y sensibilidad.
Donde,
Si en el equilibrio se considera
Entonces,
Se ha obtenido una relación no lineal, lo cual será proporcional solo cuando x << r4 =" R5" r6 =" R7" 0 =" 8.85" r =" ε" m =" NI," l =" recorrido" a =" Área">

Indice

1. Descripción de un sistema de medida y control.
2. Identificación del sistema de medida y sus bloques constitutivos.
2.1. Definición de cada bloque constitutivo
2.2. Conceptos generales sobre la medida
3. El sensor.
3.1Clasificacion.
3.2. Interferencias.
3.3. Compensación de errores
4. Características estáticas de los sistemas de medida
5. Características dinámicas.
6. Características de entrada.
7. Errores en los sistemas de medida y su análisis.
8. TEORIA DE ERRORES EN LAS MEDICIONES.
9. Error Sistemático.
10. Error Aleatorio.
11. Errores Estáticos y Errores Dinámicos.
12. Forma de expresar los errores.
12.1 Error Absoluto.
12.2 Error Relativo.
13. Cifras significativas.
14. Redondeo de Números.
15. Errores de cero, ganancia y de no linealidad.
16. Estimación del Error de una Medida Directa.
16.1 Mejor valor de un conjunto de Medidas.
16.2. Dispersión y Error. Desviación Estándar.
16.3. Significado de la Desviación Estándar. La Distribución Normal.
16.4. Medidas sin dispersión. Error de lectura o instrumental.
16.5. Propagación de Errores.
16.6. Ajuste por mínimos cuadrados

Asignacion 1 de mediciones Industriales

1. Descripción de un sistema de medida y control.

En todo proceso industrial o no, se presentan innumerables situaciones en las que se necesita conocer el estado o valor de las variables del proceso con el fin de poder actuar sobre ellas para garantizar obtener los resultados deseados.

2. Identificación del sistema de medida y sus bloques constitutivos.

Un sistema de medida es la combinación de dos o más elementos, subconjuntos y partes
Necesarias para realizar la asignación efectiva y empírica de un número a una propiedad o cualidad de un objeto o evento, de tal forma que la describa.
Toda medición exige tres funciones básicas: adquirir la información, mediante un elemento sensor o transductor, procesar dicha información y presentar los resultados, de forma que puedan ser percibidos por nuestros sentidos. Puede haber, además, transmisión, si cualquiera de estas funciones se realiza de forma remota.

2.1. Definición de cada bloque constitutivo:

Transductor: dispositivo que convierte una señal de una forma física en una señal correspondiente pero de otra forma física.
Un sensor es un dispositivo que, a partir de la energía del medio donde se mide, da una señal transducible que es función de la variable medida.
Otra distinción importante es la diferenciación entre el elemento primario y sensor electrónico.
Por ejemplo en un medidor de presión diferencial, el elemento primario es un diafragma, y su deformación se mide con el sensor electrónico.
Acondicionador: son los elementos del sistema de medida que ofrecen, a partir de la señal de salida de un sensor electrónico, una señal apta para ser presentada o registrada o simplemente permita un procesamiento posterior mediante un equipo o instrumento estándar. El acondicionador permite: amplificar, filtrar, adaptar impedancias y modular o desmodular.

2.2. Conceptos generales sobre la medida

La diferencia entre los valores máximo y mínimo de una magnitud constituye su campo o margen de variación o medida. El menor cambio que se puede discriminar se denomina resolución.
El cociente entre el margen de medida y la resolución se denomina margen dinámico (MD), y se expresa a menudo en decibelios.

3. El sensor:

Según el aporte de energía, los sensores se pueden dividir en moduladores y generadores. Según la señal de salida, los sensores se clasifican en analógicos o digitales. Atendiendo al modo de funcionamiento, los sensores pueden ser de deflexión o de comparación. En los sensores que funcionan por deflexión, la magnitud medida produce algún efecto físico, que engendra algún efecto similar, pero opuesto, en alguna parte del instrumento, y que está relacionado con alguna variable útil.

En los sensores que funcionan por comparación, se intenta mantener nula la deflexión mediante la aplicación de un efecto bien conocido, opuesto al generado por la magnitud a medir.

Según el tipo de relación entrada-salida, los sensores pueden ser de orden cero, de primer orden, de segundo orden o de orden superior ahora bien, para el estudio de un gran número de sensores se suele acudir a su clasificación de acuerdo con la magnitud medida. Se habla, en consecuencia, de sensores de temperatura, presión, caudal, humedad, posición, velocidad, aceleración, fuerza, par, etc.

Desde el punto de vista de la ingeniería electrónica, es más atractiva la clasificación de los sensores de acuerdo con el parámetro variable: resistencia, capacidad, inductancia, añadiendo luego los sensores generadores de tensión, carga o corriente, y otros tipos no incluidos en los anteriores grupos.

3.2. Interferencias.

Se denomina interferencias o perturbaciones externas aquellas señales que afectan al sistema de medida como consecuencia del principio utilizado para medir las señales de interés. Perturbaciones internas son aquellas señales que afectan indirectamente a la salida debida a su efecto sobre las características del sistema de medida.

3.3. Compensación de errores:

Los efectos de las perturbaciones internas y externas pueden reducirse mediante una alteración del diseño o a base de añadir nuevos componentes al sistema. Un método para ello es el denominado diseño con insensibilidad intrínseca. Se trata de diseñar el sistema de forma que sea inherentemente sensible sólo a las entradas deseadas.
El método de la realimentación negativa se aplica con frecuencia para reducir el efecto de las perturbaciones internas, y es el método en el que se basan los sistemas de medida por comparación. Otra técnica para reducir las interferencias es el filtrado. Un filtro es todo dispositivo que separa señales de acuerdo con su frecuencia u otro criterio. Una última técnica de compensación de perturbaciones es la utilización de entradas opuestas, que se aplica con frecuencia para compensar el efecto de las variaciones de temperatura.

4. Características estáticas de los sistemas de medida.

Exactitud (accuracy): es la capacidad de un instrumento de dar indicaciones que se
Aproximen al verdadero valor de la magnitud medida. El valor exacto se obtiene mediante métodos de medidas validados internacionalmente. La exactitud de obtiene mediante la calibración estática que no es mas que medir poco a poco una variable, y se construye entonces el patrón de referencia.
La discrepancia entre el valor correcto y el obtenido es el error.
El valor medido y su exactitud deben darse con valores numéricos compatibles, de forma que el resultado numérico de la medida no debe tener mas cifras de las que se puedan considerar validas.
20ºC + 1ºC es correcto
20ºC+0,1ºC incorrecto
20,5 ºC+1ºC incorrecto
20,5ºC+10% incorrecto

La precisión es la cualidad que caracteriza la capacidad de un instrumento de medida de dar el mismo valor de la magnitud medida, al medir varias veces en unas mismas condiciones determinadas, prescindiendo de su concordancia o discrepancia con el valor real de dicha magnitud.

La sensibilidad o factor de escala es la pendiente de la curva de calibración, que puede ser o no constante a lo largo de la escala de medida
La sensibilidad en un punto cualquiera x0 viene dada por:
S(x0) = dy/dx (evaluado en x = x0)
En los sensores se desea una alta sensibilidad y constante.

Linealidad expresa el grado de coincidencia entre la curva de calibración y una línea recta determinada. Hay varios tipos de linealidad:
i. Linealidad independiente: la línea de referencia se obtiene por el método de los mínimos cuadrados.
ii. Linealidad ajustada al cero: mínimos cuadrados pero que pase por cero
iii. Linealidad terminal
iv. Linealidad a través de los extremos.
v. Linealidad teórica: la recta es la definida por las previsiones teóricas formuladas al diseñar el sensor.

Resolución: es el incremento mínimo de la entrada para el que se obtiene un cambio en la salida.

Histéresis se refiere a la diferencia en la salida para una misma entrada, según la dirección en que se alcance.

5. Características dinámicas.

_ Error dinámico: es la diferencia entre el valor indicado y el valor exacto de la variable medida, siendo nulo el error estático.
_ La velocidad de respuesta: indica la rapidez con que el sistema de medida responde a los cambios en la variable de entrada.

La parte analógica de los sistemas de medidas mas simples se describe con un modelo matemático que consiste en una ecuación diferencial lineal con coeficientes constantes. La relación entre la salida y la entrada viene dada por la función de transferencia, que es el cociente entre las respectivas transformadas de Laplace.

La mayoría de los sensores se pueden describir con modelos de orden cero, uno o dos, y respuesta de tipo pasa bajo.

6. Características de entrada.

Las características estáticas y dinámicas no modelan en forma completa los sistemas de medida.
Está el efecto de carga que ejerce el sistema sobre el proceso bajo análisis. Cuando se definió el sistema de medida se comentó que el sensor tomaba energía del medio. Esta toma de energía altera de alguna forma el medio. Luego se puede hablar de error de carga como aquel relacionado con la alteración de la variable medida debido al sistema de medida utilizado.

7. Errores en los sistemas de medida y su análisis

Los errores de un sistema se determinan a partir de su calibración, que consiste en aplicarle entradas conocidas y comparar su salida con la obtenida con un sistema de medida de referencia, más exacto.
Según su efecto en la característica de transferencia, los errores pueden ser de cero, de ganancia y de no linealidad.
Un error de cero permanece constante con independencia del valor de la entrada. Un error de ganancia es proporcional al valor de la entrada. Un error de no linealidad hace que la característica de transferencia se aparte de una línea recta (suponiendo que sea ésta la característica ideal).

Según su naturaleza los errores pueden ser sistemáticos o aleatorios.
Un error sistemático tiene siempre la misma amplitud cuando las condiciones del sistema son las mismas, o bien varía de acuerdo con una ley conocida cuando una de dichas condiciones cambia de una forma predeterminada. Un error aleatorio tiene una magnitud que cambia de unas a otras ocasiones a pesar de que las condiciones del sistema sean las mismas.

La calibración permite corregir los errores sistemáticos y estimar la magnitud de los errores aleatorios (pero no corregirlos).
Según que se manifiesten cuando las señales de entrada son lentas o rápidas, los errores se denominan estáticos o dinámicos. Un error estático afecta a las señales lentas, por ejemplo de frecuencia inferior a 0,01 Hz. Un error dinámico afecta a las señales rápidas, y es una consecuencia de la presencia de elementos que almacenan energía. Dado que en la respuesta dinámica se consideran dos fases, la respuesta transitoria y la respuesta estacionaria, se habla de error dinámico transitorio y error dinámico estacionario.
El error dinámico de un sistema depende de su orden y de la forma de la señal de entrada. Las señales consideradas habitualmente son el escalón, la rampa y las senoidales. Los sistemas de orden cero no tienen error dinámico. Los sistemas de primer y de segundo orden tienen un error dinámico para las entradas en rampa y senoidales, incluso en régimen estacionario, y tienen un error dinámico para las entradas en escalón sólo durante la fase transitoria. En los sistemas de segundo orden la fase transitoria dura tanto más cuanto menor sea el amortiguamiento. El error dinámico para entradas senoidales incluye un retardo y un error de amplitud, pero normalmente al hablar de error dinámico se suele sobrentender el error de amplitud.

La magnitud de un error se puede expresar como error absoluto o como error relativo. El error absoluto es la diferencia entre el resultado y el verdadero valor (o valor ideal). El error relativo es el cociente entre el error absoluto y el verdadero valor. El error absoluto se expresa a veces como porcentaje de una magnitud de referencia, por ejemplo el valor de fondo de escala. La elección de una u otra forma de expresión depende del tipo de error. Los errores de cero y de no linealidad se suelen expresar como errores absolutos. Los errores de ganancia se suelen expresar como errores relativos. Dado que normalmente hay errores de todos los tipos, la expresión de la incertidumbre o error total suele incluir un término constante y otro que depende del resultado.
La incertidumbre en una magnitud que se obtiene como resultado de un cálculo en el que intervienen otras magnitudes y depende de la incertidumbre en el valor de cada una de ellas.

Por ejemplo si se quiere medir la temperatura a través de un divisor de tensión, en el cual hay una resistencia parásita R y un sensor resistivos RT, calcular la influencia de cada elemento en el valor deseado de tensión de salida.


8. TEORIA DE ERRORES EN LAS MEDICIONES

La teoría de errores constituye una rama del conocimiento científico que, a los efectos de la enseñanza, queda en un terreno intermedio entre el de las teorías científicas y el de la práctica experimental.

La limitación de los elementos físicos disponibles para realizar un sistema de medida hace que las señales de salida discrepen de las que se obtendrían con un sistema ideal. Estas discrepancias se denominan errores y, dado que algunas de ellas son inevitables, el objetivo es reducirlas de modo que a partir de la salida se pueda determinar el valor de la entrada con una incertidumbre aceptable. El número de cifras con que se exprese un resultado debe concordar con la incertidumbre que tenga asociada.

Los errores de un sistema se determinan a partir de su calibración, que consiste en aplicarle entradas conocidas y comparar su salida con la obtenida con un sistema de medida de referencia, más exacto.

Según su naturaleza los errores pueden ser sistemáticos o aleatorios.



9. Error Sistemático


Un error sistemático tiene siempre la misma amplitud cuando las condiciones del sistema son las mismas, o bien varía de acuerdo con una ley conocida cuando una de dichas condiciones cambia de una forma predeterminada.

10. Error Aleatorio

Un error aleatorio tiene una magnitud que cambia de unas a otras ocasiones a pesar de que las condiciones del sistema sean las mismas.
Los errores aleatorios se manifiestan cuando se mide repetidamente la misma magnitud con el mismo instrumento y el mismo método, y presentan las siguientes propiedades:
1. Los errores aleatorios positivos y negativos de igual valor absoluto tienen la misma probabilidad del producirse.
2. Los errores son tanto menos probables cuando mayor sea su valor.
3. Al aumentar el número de medidas, la media aritmética de los errores aleatorios de una muestra tiende a cero.
4. Para un método de medida determinado, los errores aleatorios no exceden de cierto valor.
Las medidas que lo superan deben repetirse y, en su caso, estudiarse por separado.

La calibración permite corregir los errores sistemáticos y estimar la magnitud de los errores aleatorios (pero no corregirlos)

.
11. Errores Estáticos y Errores Dinámicos

Según que se manifiesten cuando las señales de entrada son lentas o rápidas, los errores se denominan estáticos o dinámicos.

Un error estático afecta a las señales lentas, por ejemplo de frecuencia inferior a 0,01 Hz. Un error dinámico afecta a las señales rápidas, y es una consecuencia de la presencia de elementos que almacenan energía. Dado que en la respuesta dinámica se consideran dos fases, la respuesta transitoria y la respuesta estacionaria, se habla de error dinámico transitorio y error dinámico estacionario.

El error dinámico de un sistema depende de su orden y de la forma de la señal de entrada.

Las señales consideradas habitualmente son el escalón, la rampa y las senoidales. Los sistemas de orden cero no tienen error dinámico. Los sistemas de primer y de segundo orden tienen un error dinámico para las entradas en rampa y senoidales, incluso en régimen estacionario, y tienen un error dinámico para las entradas en escalón sólo durante la fase transitoria. En los sistemas de segundo orden la fase transitoria dura tanto más cuanto menor sea el amortiguamiento. El error dinámico para entradas senoidales incluye un retardo y un error de amplitud, pero normalmente al hablar de error dinámico se suele sobrentender el error de amplitud.

12. Forma de expresar los errores

La magnitud de un error se puede expresar como error absoluto, como error relativo o como error referido a fondo escala. El error absoluto es la diferencia entre el resultado y el verdadero valor (o valor ideal). El error relativo es el cociente entre el error absoluto y el verdadero valor. El error absoluto se expresa a veces como porcentaje de una magnitud de referencia, por ejemplo el valor de fondo de escala. La elección de una u otra forma de expresión depende del tipo de error.

12.1 Error Absoluto

Por motivos obvios, y por su propia naturaleza, no es posible determinar exactamente un error. En el mejor de los casos, puede llegarse a una estimación de ese error. Cuando el resultado de una medida se expresa por:

Valor medido= x= δx (unidad) (1)

lo que se quiere decir es que la magnitud medida se encuentran en el intervalo(x-δx, x+δx) con una determinada probabilidad. Con una medida logramos acotar el intervalo de valores en los que se encuentra la magnitud que pretendemos medir, pero siempre con una determinada probabilidad. Es evidente que el error expresado por δx es una magnitud de la misma clase que la medida y se expresa por tanto con la misma unidad.
También es claro que en las medidas de calidad normal el error debe ser mucho menor que el valor nominal, x. Por definición δx es siempre positivo.

12.2 Error Relativo

El error definido arriba se llama error absoluto. Tiene también interés el error relativo, que se define como el cociente del error absoluto, dividido por x.

Error relativo= δx/ x (2)

En medidas de una cierta calidad el error relativo debe ser mucho menor que la unidad.
Frecuentemente se expresa multiplicado por 100, con lo que aparece en tanto por ciento del valor medido:

Error relativo (%)= - δx/ x *100 (3)

13. Cifras significativas

Se considera que las cifras significativas de un número son aquellas que tienen significado real o aportan alguna información. Las cifras no significativas aparecen como resultado de los cálculos y no tienen significado alguno. Las cifras significativas de un número vienen determinadas por su error. Son cifras significativas aquellas que ocupan una posición igual o superior al orden o posición del error.

Una última forma de expresar el error de un número consiste en afirmar que todas sus cifras son significativas. Esto significa que el error δx es del orden de media unidad de la última cifra que se muestra. Por ejemplo, si el resultado de una medida de longitud es de 5432,8 m, y afirmamos que todas las cifras son significativas, quiere decirse que el error es del orden de 0,5 m, puesto que la última cifra mostrada es del orden de las décimas de metro.
¿Cómo pueden determinarse las cifras significativas a partir del número que expresa el error?
Hay que tener siempre presente que todo error es una estimación y está por tanto sujeto a su vez a una incertidumbre, generalmente grande. Por esto no tiene sentido especificarlo con excesiva precisión. Salvo casos excepcionales, se expresará con una sola cifra significativa.

14. Redondeo de Números

Hemos visto que todos los números resultantes de una medida tienen una cierta incertidumbre. Es necesario eliminar de estos números aquellas cifras que carecen de significado porque el error es mayor que lo que estas cifras significan.

Las reglas que se emplean en el redondeo de números son las siguientes:
_ Si la cifra que se omite es menor que 5, se elimina sin más.
_ Si la cifra eliminada es mayor que 5, se aumenta en una unidad la última cifra retenida.
_ Si la cifra eliminada es 5, se toma como última cifra el número par más próximo; es decir, si la cifra retenida es par se deja, y si es impar se toma la cifra superior.
_ Algunos ejemplos. Si redondeamos 3,678 a tres cifras significativas, el resultado es
3,68, que está más cerca del original que 3,67. En cambio si el número a redondear, también a tres cifras, fuera 3,673, quedaría 3,67 que es más próximo al original que 3,68. Para redondear 3,675, según la tercera regla, debemos dejar 3,68.
Las dos primeras reglas son de sentido común. La tercera es un convenio razonable porque, si se sigue siempre, la mitad de las veces redondeamos por defecto y la mitad por exceso.

Cuando los números a redondear sean grandes, las cifras eliminadas se sustituyen por ceros.

15. Errores de cero, ganancia y de no linealidad

Según su efecto en la característica de transferencia, los errores pueden ser de cero, de ganancia y de no linealidad.

Un error de cero permanece constante con independencia del valor de la entrada. Un error de ganancia es proporcional al valor de la entrada. Un error de no linealidad hace que la característica de transferencia se aparte de una línea recta (suponiendo que sea ésta la característica ideal).

Los errores de cero y de no linealidad se suelen expresar como errores absolutos. Los errores de ganancia se suelen expresar como errores relativos. Dado que normalmente hay errores de todos los tipos, la expresión de la incertidumbre o error total suele incluir un término constante y otro que depende del resultado.

16. Estimación del Error de una Medida Directa

La estimación del error de una medida tiene siempre una componente subjetiva. En efecto, nadie mejor que un observador experimentado para saber con buena aproximación cuál es el grado de confianza que le merece la medida que acaba de tomar. No existe un conjunto de reglas bien fundadas e inalterables que permitan determinar el error de una medida en todos los casos imaginables. Muchas veces es tan importante consignar cómo se ha obtenido un error como su propio valor.

16.1 Mejor valor de un conjunto de Medidas

Supongamos que medimos una magnitud un número n de veces. Debido a la existencia de errores aleatorios, las n medidas x1, x2,…, xn serán en general diferentes.
El método más razonable para determinar el mejor valor de estas medidas es tomar el valor medio. En efecto, si los errores son debidos al azar, tan probable es que ocurran por defecto como por exceso, y al hacer la media se compensarán, por lo menos parcialmente. El valor medio se define por:
n
X= (1/n) ∑ x1 (4)
i=1
y este es el valor que deberá darse como resultado de las medidas.


16.2. Dispersión y Error. Desviación Estándar


Evidentemente, el error de la medida debe estar relacionado con la dispersión de los valores; es decir, si todos los valores obtenidos en la medición son muy parecidos, es lógico pensar que el error es pequeño, mientras que si son muy diferentes, el error debe ser mayor.

Adoptando un criterio pesimista, podría decirse que el error es la semidiferencia entre el valor máximo y el mínimo.
σ (5)

Cuando el número de datos es pequeño, suele preferirse el cálculo de la desviación estándar por la ecuación:
La primera suele llamarse desviación estándar de población, y la segunda desviación estándar muestral.

16.3. Significado de la Desviación Estándar. La Distribución Normal

Los valores de la desviación estándar que hemos calculado en la sección anterior, son realmente estimadores de este parámetro. El conjunto de las medidas de una magnitud, siempre que exista un error accidental, pueden caracterizarse por medio de una distribución estadística. Cuando el error es debido a un gran número de pequeñas causas independientes, la distribución se aproxima a la llamada distribución normal.

La forma de representar en estadística una distribución es representando en abscisas el conjunto de valores que pueden obtenerse en una medida y en ordenadas la probabilidad de obtenerlos. En el caso de que la magnitud medida varíe de forma continua, en ordenadas se representa la probabilidad por unidad de intervalo de la magnitud medida. En una distribución continua, la probabilidad de que una medida esté entre dos valores x0 y x1 viene representada por:

P= (7)


Donde f(x) es la función de densidad de la distribución. La función de densidad representa la probabilidad (por unidad de intervalo de la magnitud medida) de obtener un determinado valor en una medida. Obviamente:

P= (8)

puesto que es seguro (probabilidad 1) obtener un valor cualquiera cuando se mide una magnitud.

16.4. Medidas sin dispersión. Error de lectura o instrumental


En ocasiones la repetición de la medida de una magnitud conduce siempre al mismo valor.

En efecto, el hecho de que todas las medidas sean iguales no indica en general que no haya error accidental, sino que éste es demasiado pequeño para quedar reflejado en el aparato.

Se llama sensibilidad de un aparato a la mínima variación de la magnitud medida que es capaz de detectar. En los instrumentos analógicos coincide frecuentemente con la mínima división de la escala.

Suele llamarse apreciación al máximo error que puede cometerse debido a la sensibilidad del aparato. Generalmente se considera como la mitad de la sensibilidad.

En resumen, el error instrumental de una medida se expresa frecuentemente por:

Eins = s/3 (9)

Donde: s es la sensibilidad del aparato de medida.

En aquellos casos en que los errores sean del mismo orden de magnitud, puede considerarse que el error total es la suma de los dos:
E= eins + σ (10)

donde eins es el error instrumental y σ es el error accidental expresado por la desviación estándar.

16.5. Propagación de Errores

Las operaciones matemáticas con números inciertos dan lugar a resultados también inciertos, y es importante poder estimar el error de los resultados a partir de los errores de los números con los que se opera.

16.6. Ajuste por mínimos cuadrados

Hasta ahora nos hemos ocupado de la manera de obtener el mejor valor de una magnitud a partir de una o varias medidas. Un problema más general es determinar la relación funcional entre dos magnitudes x e y como resultado de experimentos.
Supongamos que por razones teóricas bien fundadas sabemos que entre x e y existe la relación lineal
y=ax+b
y deseamos determinar los parámetros a y b a partir de n medidas de x e y. a es la pendiente de la recta, es decir, la tangente del ángulo que forma con el eje de abscisas, y b la ordenada en el origen, es decir la altura a la que corta la recta al eje de ordenadas.
Para concretar, supongamos que los valores que han resultado de un experimento son los siguientes:

X1 1 2 3 4 5 6
Y1 1.5 2.5 4.0 3.6 5.9 6.1

Para determinar la recta que mejor se adapta a los puntos se emplea el llamado método de los mínimos cuadrados. Para un valor de x determinado, la recta de ajuste proporciona un valor diferente de y del medido en el experimento. Esta diferencia será positiva para algunos puntos y negativa para otros, puesto que los puntos se disponen alrededor de la recta. Por este motivo, la suma de estas diferencias para todos los puntos es poco significativa (las diferencias negativas se compensan con las positivas).

Por ello, para medir la discrepancia entre la recta y los puntos, se emplea la suma de los cuadrados de las diferencias, con los que nos aseguramos de que todos los términos son positivos. Esta suma tiene la forma:
Φ= (14)